半分以上隠れている円の直径の推定
- 顕微鏡写真で,重なっていて半分以上見えない粒子の粒径を推定したい
-
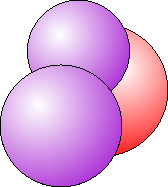
- 赤い円は半分以上が隠れているため,直径を直接測定することができない。
-
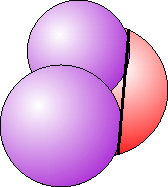
- 赤い円になるべく長い弦を引く。途中は手前の円を横切ってもよい。
-
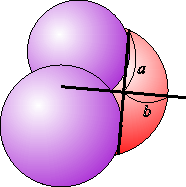
- その弦に垂直二等分線を引く。線分 \(a\) および \(b\) の長さは測定可能。
-
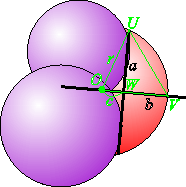
- 赤い円の見えない中心を \(O\),円弧状の点をそれぞれ\(U\),\(V\),弦と垂直二等分線の交点を\(W\) とする。
- 線分\(\overline{OW}\) の長さを \(c\) とする。
- 線分\(\overline{OU}\) の長さは半径 \(r\) に等しい。
-
- ピタゴラスの定理から
- \(r^2 = a^2 + c^2 \tag{1}\)
-
- 線分OV の長さもまた半径 r に等しいので,
- \(c = r - b\)
-
- これを式(1)に代入すると
- \begin{align}
r^2 &= a^2 + (r - b)^2\\
&= a^2 + r^2 - 2 rb + b^2
\end{align}
- ゆえに
- \(r = \displaystyle \frac{a^2+b^2}{2b}\)
- 直径は \(D=2r\) であるから
- \(D = \displaystyle \frac{a^2+b^2}{b}\)
- このように線分 \(a\) および \(b\) の長さから直径 \(D\) を推定できる。
-
半分以上隠れている円の直径の推定







