接触角の概算
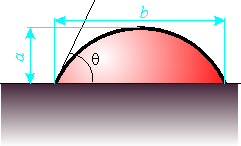
- 固体に接触する液体の接触角 \(\theta\) を求めたい。
- 写真から直接角度を測定するのは難しい。それに対して長さを測定するのは簡単である。液体の高さ \(a\) と,液体が固体と接触している辺の長さ \(b\) から概算する。
-
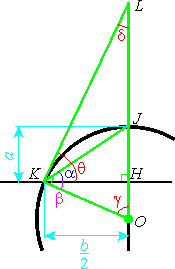
- 液体は円の一部と見なす。
-
- 円の中心 \(O\) から点 \(J\) を通る線を引き,接線との交点を \(L\) とする。
-
- \(\triangle OLK\) と \(\triangle KLH\) は共に直角三角形で,一つの角 \(\delta\) は共有であるから,互いに相似である。したがって,それぞれの余角 \(\theta\) と \(\gamma\) は等しい。
- \(\theta = \gamma\)
-
- \(\triangle OKH\) もまた直角三角形で,一つの角 \(\gamma\) は \(\triangle OLK\) と共有であるから,互いに相似である。内角の和は \(\pi\) であるから
- \(\beta + \gamma + \displaystyle \frac{\pi}{2}= \pi \tag{1}\)
-
- 線分 \(\overline{OK}\) と線分 \(\overline{OJ}\) はどちらも半径であるから, \(\triangle OJK\) は二等辺三角形である。
- \(2 (\alpha + \beta) + \gamma = \pi \tag{2}\)
-
- 式(1)と(2)を連立して解けば
- \(\gamma = 2\alpha = \theta \)
-
- \begin{align}
\tan \alpha &= \displaystyle \frac {a} {b/2}\\
\alpha &= \tan^{-1} \displaystyle \frac {2a} {b}
\end{align}
-
- \(\therefore \theta = 2 \tan^{-1} \displaystyle \frac {2a} {b}\)
接触角の概算



